/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Równania z pierwiastkami

Zadanie nr 2296395

Dla jakich wartości parametru 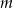m suma pierwiastków równania 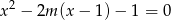x 2 − 2m (x − 1) − 1 = 0 jest równa sumie kwadratów tych pierwiastków?

Wersja PDF

Rozwiązanie

Zapiszmy równanie w postaci ogólnej.

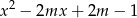
2 x − 2mx + 2m − 1

Sprawdźmy kiedy równanie ma pierwiastki.

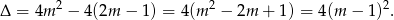
2 2 2 Δ = 4m − 4(2m − 1 ) = 4(m − 2m + 1) = 4(m − 1) .

Zatem 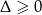Δ ≥ 0 , czyli równanie zawsze ma pierwiastki. Na mocy wzorów Vi‘ete’a mamy

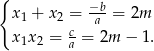
{ x1 + x2 = −ab-= 2m x x = c = 2m − 1. 1 2 a

Musimy zatem rozwiązać równanie:

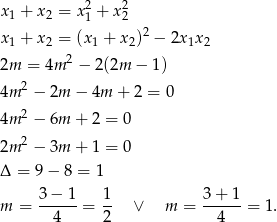
2 2 x1 + x2 = x 1 + x 2 x1 + x2 = (x 1 + x 2)2 − 2x 1x2 2 2m = 4m − 2(2m − 1) 4m 2 − 2m − 4m + 2 = 0 4m 2 − 6m + 2 = 0 2 2m − 3m + 1 = 0 Δ = 9− 8 = 1 3 − 1 1 3+ 1 m = ------= -- ∨ m = ------= 1. 4 2 4

Zauważmy, że powyższy rachunek ma sens również w przypadku, gdy równanie ma pierwiastek podwójny, czyli dla 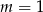m = 1 . W tej sytuacji mamy jeden pierwiastek 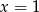x = 1 , który jest równy swojemu kwadratowi.  
Odpowiedź: 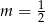1 m = 2 lub m = 1

Wersja PDF