Zadanie nr 2999482
Dany jest trójmian kwadratowy 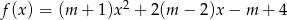 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 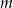 , dla których trójmian
, dla których trójmian 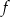 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 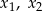 , spełniające warunek
, spełniające warunek 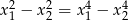 .
.
Rozwiązanie
Jeżeli funkcja 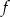 ma mieć dwa różne pierwiastki, to musi to być funkcja kwadratowa, czyli
ma mieć dwa różne pierwiastki, to musi to być funkcja kwadratowa, czyli 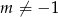 . Sprawdzamy teraz, kiedy równanie ma dwa różne pierwiastki.
. Sprawdzamy teraz, kiedy równanie ma dwa różne pierwiastki.
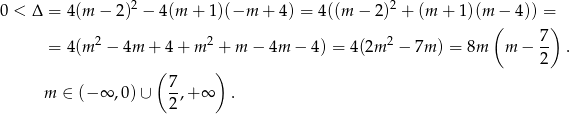
Przy powyższym założeniu możemy zapisać wzory Vièteá
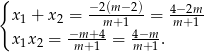
Przekształćmy teraz dany warunek tak, aby móc zastosować wzory Viète’a. Zauważmy, że założyliśmy, że 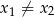 , więc możemy dzielić przez
, więc możemy dzielić przez 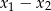 . Zauważmy ponadto, że gdyby
. Zauważmy ponadto, że gdyby 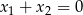 , to z powyższych wzorów Viète’a mielibyśmy
, to z powyższych wzorów Viète’a mielibyśmy 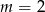 , a to jest sprzeczne z warunkiem na
, a to jest sprzeczne z warunkiem na 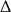 –ę. Możemy więc dzielić przez
–ę. Możemy więc dzielić przez 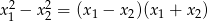 .
.
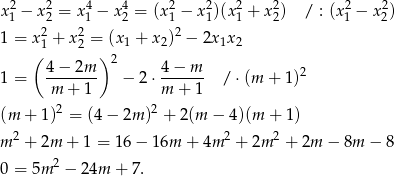
Rozwiązujemy otrzymane równanie kwadratowe.
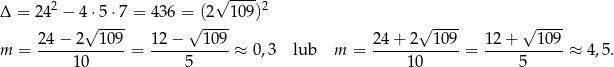
Tylko drugie z tych rozwiązań spełnia warunek z 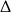 –ą.
–ą.
Odpowiedź: