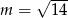Zadanie nr 3743653
Wyznacz wszystkie wartości parametru 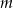 , dla których równanie
, dla których równanie 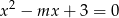 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 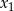 i
i 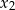 takie, że
takie, że 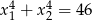 .
.
Rozwiązanie
Sprawdźmy kiedy równanie ma dwa pierwiastki rzeczywiste.
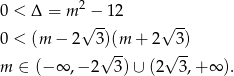
Spróbujmy teraz zapisać sumę czwartych potęg przy pomocy sumy i iloczynu tak, aby móc skorzystać ze wzorów Viète’a.
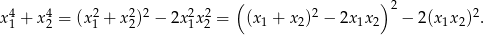
Teraz korzystamy ze wzorów Viète’a.
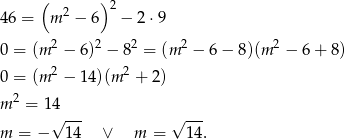
Łatwo sprawdzić, że obie te liczby spełniają warunek z 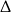 -ą.
-ą.
Odpowiedź: 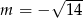 lub
lub