/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Równania z pierwiastkami

Zadanie nr 4231254

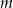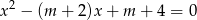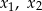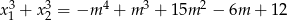Oblicz wszystkie wartości parametru m , dla których równanie x 2 − (m + 2)x + m + 4 = 0 ma dwa różne pierwiastki rzeczywiste x 1, x2 takie, że x31 + x32 = −m 4 + m 3 + 15m 2 − 6m + 12 .

Wersja PDF

Rozwiązanie

Sprawdźmy najpierw kiedy równanie ma dwa różne pierwiastki

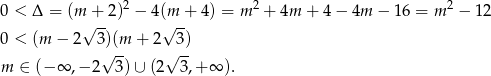
2 2 2 0 < Δ = (m√+-2) − 4(√m-+ 4) = m + 4m + 4 − 4m − 16 = m − 12 0 < (m − 2 3)(m + 2 3 ) √ -- √ -- m ∈ (− ∞ ,− 2 3) ∪ (2 3,+ ∞ ).

Korzystamy teraz ze wzorów Viète’a

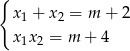
{ x1 + x2 = m + 2 x1x2 = m + 4

Ponieważ

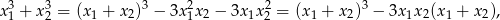
x3+ x3 = (x + x )3 − 3x2x − 3x x2 = (x + x )3 − 3x x (x + x ), 1 2 1 2 1 2 1 2 1 2 1 2 1 2

musimy więc rozwiązać równanie.

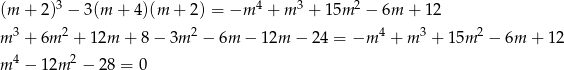
3 4 3 2 (m + 2 ) − 3(m + 4)(m + 2) = −m + m + 15m − 6m + 12 m 3 + 6m 2 + 12m + 8 − 3m 2 − 6m − 1 2m − 2 4 = −m 4 + m 3 + 15m 2 − 6m + 12 m 4 − 1 2m 2 − 28 = 0

Podstawiamy teraz 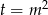2 t = m .

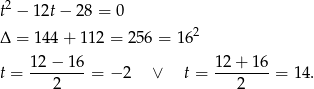
2 t − 12t − 28 = 0 Δ = 14 4+ 1 12 = 256 = 162 t = 12−--16-= − 2 ∨ t = 12-+-16-= 14. 2 2

Ujemne rozwiązanie odrzucamy i mamy

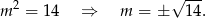
2 √ --- m = 14 ⇒ m = ± 14 .

Oczywiście liczby te spełniają warunek z 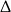Δ -ą: 2 m > 12 .  
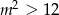Odpowiedź: 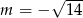√ --- m = − 14 lub √ --- m = 14

Wersja PDF