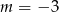/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Równania z pierwiastkami

Zadanie nr 4485187

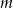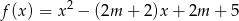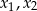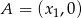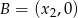Wyznacz wszystkie wartości parametru m , dla których funkcja kwadratowa f (x) = x2 − (2m + 2)x + 2m + 5 ma dwa różne pierwiastki x 1,x2 takie, że suma kwadratów odległości punktów A = (x1,0) i B = (x2,0) od prostej o równaniu 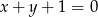x+ y+ 1 = 0 jest równa 6.

Wersja PDF

Rozwiązanie

Sprawdźmy na początek, kiedy dana funkcja 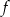f ma dwa różne pierwiastki x1,x 2 .

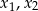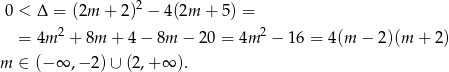
2 0 < Δ = (2m + 2) − 4(2m + 5) = = 4m 2 + 8m + 4− 8m − 2 0 = 4m 2 − 16 = 4(m − 2)(m + 2) m ∈ (− ∞ ,− 2)∪ (2,+ ∞ ).

Przy tym założeniu równanie ma dwa różne pierwiastki spełniające wzory Viète’a

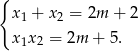
{ x1 + x2 = 2m + 2 x1x 2 = 2m + 5.

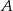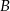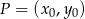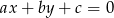Pozostało teraz sprawdzić, kiedy suma kwadratów odległości punktów A i B od danej prostej jest równa 6. Korzystamy ze wzoru na odległość punktu P = (x0,y0) od prostej ax+ by+ c = 0 :

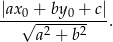
|ax0√-+-by-0 +-c|. a2 + b2

W naszej sytuacji mamy równanie

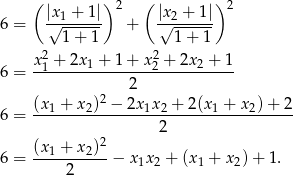
( ) 2 ( ) 2 6 = |√x1 +-1| + |x√2-+-1|- 1 + 1 1+ 1 x 2+ 2x + 1+ x 2+ 2x + 1 6 = --1-----1--------2-----2---- 2 (x-1 +-x-2)2 −-2x-1x2 +-2(x1 +-x2)+-2 6 = 2 2 6 = (x-1 +-x-2)-− x1x2 + (x1 + x2)+ 1. 2

Korzystamy teraz ze wzorów Viète’a.

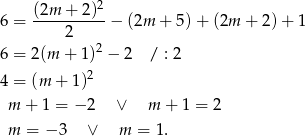
2 6 = (2m-+-2)--− (2m + 5) + (2m + 2)+ 1 2 6 = 2(m + 1)2 − 2 / : 2 2 4 = (m + 1) m + 1 = − 2 ∨ m + 1 = 2 m = − 3 ∨ m = 1.

Tylko pierwsza z tych liczb spełnia warunek z 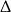Δ -ą.  
Odpowiedź: m = − 3

Wersja PDF