Zadanie nr 4999320
Liczby 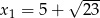 i
i 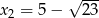 są rozwiązaniami równania
są rozwiązaniami równania 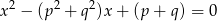 z niewiadomą
z niewiadomą  . Oblicz wartości
. Oblicz wartości 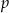 i
i 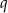 .
.
Rozwiązanie
Na mocy wzorów Viète’a mamy
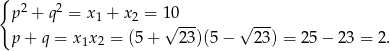
Sposób I
Musimy rozwiązać powyższy układ równań. Wstawiamy 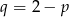 do pierwszego równania
do pierwszego równania
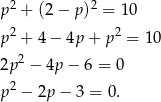
Dalej 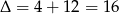 i
i 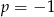 lub
lub 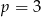 . Wtedy
. Wtedy 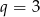 lub
lub 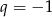 odpowiednio.
odpowiednio.
Sposób II
Ponieważ
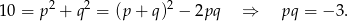
Zatem na mocy wzorów Viète’a liczby 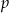 i
i 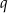 są pierwiastkami równania
są pierwiastkami równania
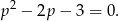
Równanie to rozwiązujemy tak jak poprzednio. 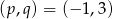 lub
lub 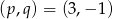 .
.

