/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Równania z pierwiastkami

Zadanie nr 5534497

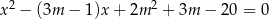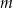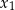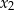Dane jest równanie kwadratowe 2 2 x − (3m − 1)x + 2m + 3m − 20 = 0 z niewiadomą x . Wyznacz wszystkie wartości parametru m , dla których różne rozwiązania x1 i x 2 tego równania istnieją i spełniają warunek

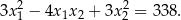
3x 21 − 4x1x2 + 3x22 = 3 38.
Wersja PDF

Rozwiązanie

Sprawdźmy najpierw kiedy równanie ma dwa różne pierwiastki.

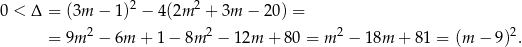
2 2 0 < Δ = (3m − 1) − 4(2m + 3m − 2 0) = = 9m 2 − 6m + 1− 8m 2 − 12m + 80 = m 2 − 18m + 81 = (m − 9)2.

Musi więc być 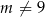m ⁄= 9 . Przy tym założeniu możemy zapisać wzory Viète’a

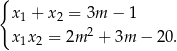
{ x1 + x2 = 3m − 1 x x = 2m 2 + 3m − 20 . 1 2

Przekształćmy teraz podaną równość.

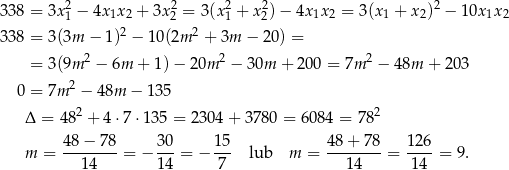
2 2 2 2 2 338 = 3x 1 − 4x1x2 + 3x2 = 3(x1 + x2)− 4x1x2 = 3(x 1 + x 2) − 1 0x1x2 338 = 3 (3m − 1 )2 − 10 (2m 2 + 3m − 20) = 2 2 2 = 3 (9m − 6m + 1) − 20m − 30m + 200 = 7m − 48m + 203 0 = 7m 2 − 48m − 135 Δ = 482 + 4 ⋅7⋅ 135 = 23 04+ 3780 = 6 084 = 782 m = 48−--78-= − 3-0 = − 15- lub m = 48-+-78-= 126-= 9. 14 1 4 7 1 4 14

Rozwiązanie 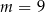m = 9 nie spełnia warunku z 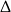Δ -ą, więc jedyne rozwiązanie to m = − 15 7 .  
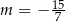Odpowiedź: 15 m = − 7

Wersja PDF