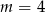/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Równania z pierwiastkami

Zadanie nr 5608582

Wyznacz wszystkie wartości parametru 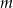m , dla których równanie 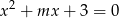x 2 + mx + 3 = 0 ma dwa różne pierwiastki rzeczywiste, takie, że suma ich czwartych potęg jest równa 82.

Wersja PDF

Rozwiązanie

Sprawdźmy kiedy równanie ma dwa pierwiastki rzeczywiste.

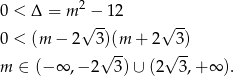
2 0 < Δ = m √−--12 √ -- 0 < (m − 2 3)(m + 2 3) √ -- √ -- m ∈ (− ∞ ,−2 3)∪ (2 3 ,+∞ ).

Spróbujmy teraz zapisać sumę czwartych potęg przy pomocy sumy i iloczyny tak, aby móc skorzystać ze wzorów Viète’a.

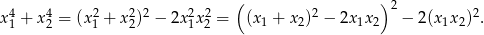
4 4 2 2 2 2 2 ( 2 )2 2 x1 + x2 = (x 1 + x 2) − 2x 1x2 = (x 1 + x 2) − 2x 1x2 − 2(x1x 2).

Teraz korzystamy ze wzorów Viète’a.

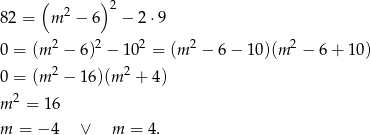
( 2 ) 2 82 = m − 6 − 2 ⋅9 2 2 2 2 2 0 = (m − 6 ) − 1 0 = (m − 6 − 10 )(m − 6 + 10) 0 = (m 2 − 1 6)(m 2 + 4) m2 = 16 m = − 4 ∨ m = 4.

Łatwo sprawdzić, że obie te liczby spełniają warunek z Δ -ą.  
Odpowiedź: 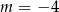m = − 4 lub m = 4

Wersja PDF