/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Równania z pierwiastkami

Zadanie nr 5691984

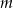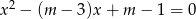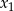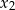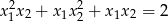Wyznacz te wartości parametru m , dla których równanie 2 x − (m − 3)x+ m − 1 = 0 ma dwa rozwiązania x1 i x2 spełniające warunek x21x 2 + x 1x22 + x1x2 = 2 .

Wersja PDF

Rozwiązanie

Powinniśmy zacząć od sprawdzenia kiedy równanie ma dwa pierwiastki, ale zostawimy to sobie na koniec (sprawdzimy otrzymane wartości 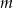m ). Na mocy wzorów Viète’a mamy

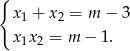
{ x1 + x2 = m − 3 x1x2 = m − 1.

Przekształćmy teraz podaną równość.

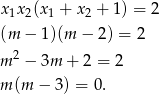
x1x 2(x 1 + x 2 + 1 ) = 2 (m − 1)(m − 2 ) = 2 2 m − 3m + 2 = 2 m (m − 3) = 0.

Pozostało sprawdzić czy dla tych wartości 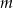m równanie ma dwa pierwiastki. Mamy odpowiednio równania

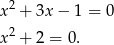
x2 + 3x − 1 = 0 x2 + 2 = 0 .

Zatem dwa pierwiastki są tylko dla 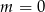m = 0 .  
Odpowiedź: m = 0

Wersja PDF