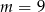/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Równania z pierwiastkami

Zadanie nr 6012077

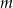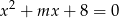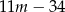Wyznacz wszystkie wartości parametru m , dla których równanie x 2 + mx + 8 = 0 ma dwa różne pierwiastki rzeczywiste takie, że suma ich kwadratów jest równa 1 1m − 34 .

Wersja PDF

Rozwiązanie

Na początku sprawdźmy kiedy równanie ma dwa różne pierwiastki.

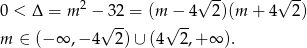
2 √ -- √ -- 0 < Δ = m − √32-= (m√−--4 2)(m + 4 2) m ∈ (− ∞ ,−4 2)∪ (4 2 ,+∞ ).

Na mocy wzorów Viète’a mamy

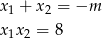
x1 + x2 = −m x1x2 = 8

Podany warunek daje nam więc równanie.

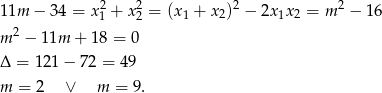
2 2 2 2 11m − 34 = x1 + x2 = (x1 + x2) − 2x1x2 = m − 16 m 2 − 1 1m + 18 = 0 Δ = 121− 72 = 49 m = 2 ∨ m = 9.

Dla 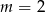m = 2 równanie nie ma rozwiązań, natomiast 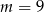m = 9 jest OK.  
Odpowiedź: m = 9

Wersja PDF