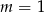/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Równania z pierwiastkami

Zadanie nr 7420367

Znajdź takie wartości parametru 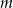m , aby połowa jednego pierwiastka równania 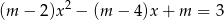(m − 2)x2 − (m − 4)x + m = 3 była równa odwrotności drugiego pierwiastka.

Wersja PDF

Rozwiązanie

Warunek o którym mowa w treści zadania możemy zapisać w postaci

x 1 -1-= --- ⇒ x1x2 = 2. 2 x2

Na mocy wzorów Viète’a jest to równoważne warunkowi

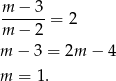
m − 3 ------ = 2 m − 2 m − 3 = 2m − 4 m = 1.

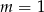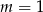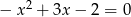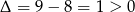Na koniec należy sprawdzić czy dla m = 1 równanie rzeczywiście ma pierwiastki (jest to prostsze niż ustalanie kiedy równanie ma pierwiastki, dlatego nie zrobiliśmy tego na początku). Dla m = 1 mamy równanie − x2 + 3x − 2 = 0 i Δ = 9 − 8 = 1 > 0 .  
Odpowiedź: m = 1

Wersja PDF