/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Równania z pierwiastkami

Zadanie nr 8322814

Dla jakich wartości parametru 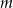m jeden z pierwiastków równania 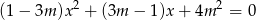(1 − 3m )x2 + (3m − 1)x + 4m 2 = 0 jest połową drugiego pierwiastka?

Wersja PDF

Rozwiązanie

Sprawdzamy najpierw kiedy równanie ma dwa pierwiastki. Oczywiście musi być 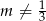m ⁄= 13 oraz

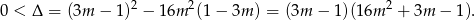
0 < Δ = (3m − 1)2 − 16m 2(1 − 3m ) = (3m − 1)(16m 2 + 3m − 1).

Na razie zostawmy ten warunek w tej postaci – zamiast rozwiązywać tę nierówność na koniec sprawdzimy, czy jest ona spełniona przez otrzymane wartości 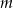m .

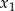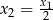Jeżeli x1 i x2 = x12 są pierwiastkami danego równania to na mocy wzorów Viète’a mamy

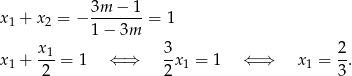
3m--−-1 x1 + x2 = − 1 − 3m = 1 x 3 2 x1 + -1-= 1 ⇐ ⇒ --x1 = 1 ⇐ ⇒ x1 = -. 2 2 3

Zatem 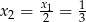x1- 1 x2 = 2 = 3 i na mocy drugiego wzoru Viète’a mamy

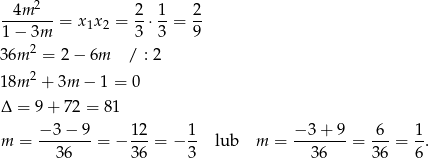
4m 2 2 1 2 ------- = x1x 2 = --⋅--= -- 1− 3m 3 3 9 36m 2 = 2 − 6m / : 2 2 18m + 3m − 1 = 0 Δ = 9 + 7 2 = 81 m = −-3−--9 = − 1-2 = − 1- lub m = −-3+--9 = -6- = 1-. 36 3 6 3 36 3 6 6

Na koniec sprawdzamy, że otrzymane liczby spełniają warunek z 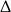Δ -ą.

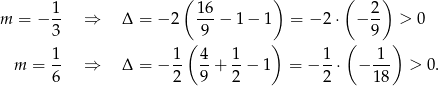
( ) ( ) 1 16 2 m = − -- ⇒ Δ = − 2 ---− 1 − 1 = − 2 ⋅ − -- > 0 3 ( 9 ) ( 9 ) 1- 1- 4- 1- 1- 1-- m = 6 ⇒ Δ = − 2 9 + 2 − 1 = − 2 ⋅ − 18 > 0.

 
Odpowiedź: 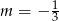m = − 13 lub m = 16

Wersja PDF