Zadanie nr 8620539
Wyznacz wszystkie wartości parametru 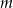 , dla których równanie
, dla których równanie 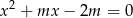 ma dwa różne rozwiązania rzeczywiste
ma dwa różne rozwiązania rzeczywiste 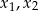 spełniające warunek
spełniające warunek 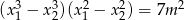 .
.
Rozwiązanie
Sprawdzamy najpierw, kiedy równanie ma dwa różne pierwiastki
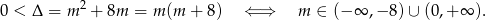
Przy tym założeniu możemy napisać wzory Viète’a.
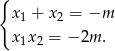
Spróbujemy teraz przekształcić lewą stronę podanej równości, tak aby móc skorzystać ze wzorów Viète’a. Zrobimy to na dwa sposoby.
Sposób I
Zauważmy, że
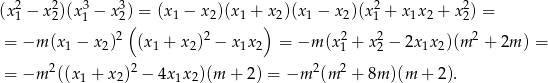
Pozostało teraz rozwiązać równanie
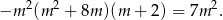
Oczywiście jednym z rozwiązań jest 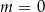 , ale liczba ta nie spełnia warunku z
, ale liczba ta nie spełnia warunku z 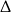 -ą, więc możemy założyć, że
-ą, więc możemy założyć, że 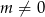 i podzielić równanie stronami przez
i podzielić równanie stronami przez 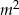 .
.
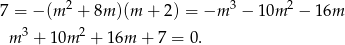
Szukamy teraz wymiernych pierwiastków tego równania – sprawdzamy dzielniki wyrazu wolnego. Jednym z pierwiastków jest 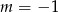 , więc dzielimy wielomian z lewej strony przez
, więc dzielimy wielomian z lewej strony przez 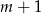 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
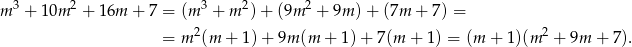
Rozkładamy teraz trójmian w nawiasie.
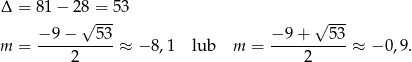
W takim razie jedyną wartością 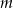 spełniającą warunki zadania jest
spełniającą warunki zadania jest 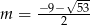 .
.
Sposób II
Zauważmy najpierw, że
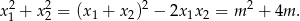
Przekształcamy teraz lewą stronę danej równości. Zauważmy, że
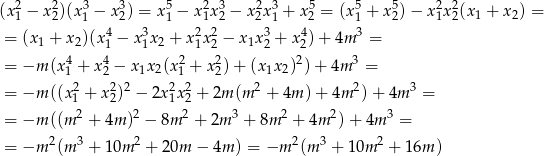
Dalszą część rozwiązania przeprowadzamy dokładnie tak samo jak w poprzednim sposobie.
Odpowiedź: