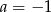Zadanie nr 9796789
Wyznacz te wartości parametru  , dla których różne pierwiastki
, dla których różne pierwiastki 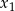 i
i 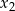 równania
równania 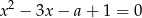 spełniają warunek
spełniają warunek 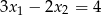 .
.
Rozwiązanie
Sposób I
Powinniśmy zacząć od sprawdzenia kiedy dane równanie ma dwa różne pierwiastki. Zostawimy to jednak sobie na koniec – sprawdzimy czy otrzymane wartości  są poprawne.
są poprawne.
Ze wzorów na pierwiastki mamy
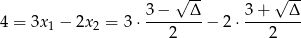
lub
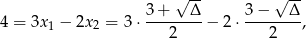
gdzie 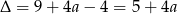 . Rozwiążemy oba te równania.
. Rozwiążemy oba te równania.
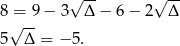
Równanie to jest oczywiście sprzeczne. Teraz druga możliwość
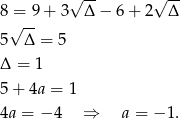
Z powyższego rachunku jest jasne, że dla 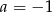 , mamy
, mamy 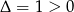 .
.
Sposób II
Podobnie jak poprzednio, sprawdzenie czy 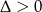 zostawmy sobie na koniec. Na mocy wzorów Viète’a mamy
zostawmy sobie na koniec. Na mocy wzorów Viète’a mamy 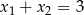 co daje nam układ równań
co daje nam układ równań
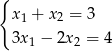
Dodając do drugiego równania podwojone pierwsze (żeby skrócić 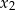 ) mamy
) mamy
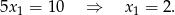
Zatem 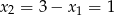 . Sprawdźmy teraz kiedy
. Sprawdźmy teraz kiedy 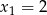 jest pierwiastkiem
jest pierwiastkiem
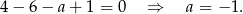
Na koniec musimy jeszcze sprawdzić, czy 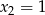 jest pierwiastkiem – jeżeli to zrobimy, nie musimy już sprawdzać
jest pierwiastkiem – jeżeli to zrobimy, nie musimy już sprawdzać 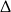 -y.
-y.
Odpowiedź: