Zadanie nr 2138987
Wyznacz wszystkie wartości 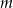 , dla których równanie
, dla których równanie 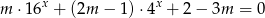 nie ma pierwiastków rzeczywistych.
nie ma pierwiastków rzeczywistych.
Rozwiązanie
Jeżeli podstawimy 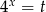 to mamy równanie
to mamy równanie
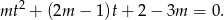
Jeżeli 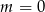 to mamy równanie
to mamy równanie 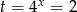 , które ma rozwiązanie
, które ma rozwiązanie 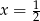 , dlatego załóżmy dalej, że
, dlatego załóżmy dalej, że 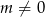 .
.
Jeżeli zapiszemy równość 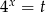 w postaci
w postaci

to widać, że równanie nie będzie miało rozwiązań, gdy powyższe równanie kwadratowe nie ma rozwiązań lub gdy rozwiązania są niedodatnie.
Sprawdźmy najpierw kiedy 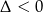 .
.
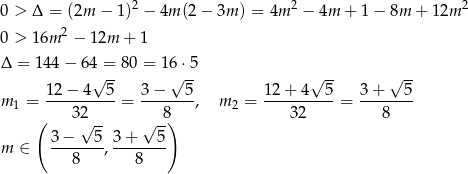
Jeżeli 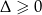 to sprawdzamy ze wzorów Viéte’a, kiedy rozwiązania są niedodatnie.
to sprawdzamy ze wzorów Viéte’a, kiedy rozwiązania są niedodatnie.
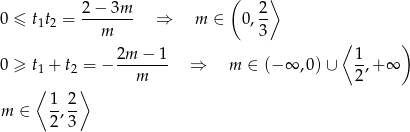
Ponieważ
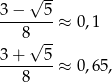
to
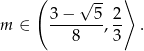
Odpowiedź: