Zadanie nr 4883532
Określ funkcję która każdemu argumentowi 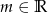 przyporządkowuje liczbę rozwiązań równania
przyporządkowuje liczbę rozwiązań równania
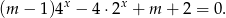
Naszkicuj wykres tej funkcji.
Rozwiązanie
Podstawiając 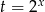 mamy równanie
mamy równanie
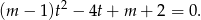
Jeżeli zapiszemy warunek 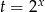 w postaci
w postaci
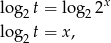
to widać, że ilość rozwiązań wyjściowego równania jest taka sama jak ilość dodatnich rozwiązań powyższego równania kwadratowego.
Sprawdźmy najpierw co się dzieje gdy równanie to nie jest kwadratowe, czyli dla 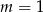 . Mamy wtedy
. Mamy wtedy
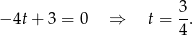
Jest zatem jedno rozwiązanie dodatnie.
Sprawdźmy teraz kiedy równanie w ogóle nie ma rozwiązań.
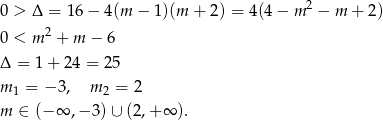
Sprawdźmy teraz co się dzieje jak są pierwiastki. Na początku ustalmy kiedy są one niedodatnie (wtedy wyjściowe równanie nie ma rozwiązań). Na mocy wzorów Viéte’a tak będzie gdy
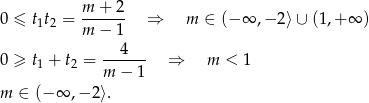
W połączeniu z warunkiem z  -ą oznacza to, że równanie nie ma rozwiązań dla
-ą oznacza to, że równanie nie ma rozwiązań dla
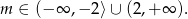
Sprawdźmy teraz kiedy jest jedno, a kiedy są dwa rozwiązania dodatnie. Jeszcze raz korzystając ze wzorów Viéte’a, dwa rozwiązania dodatnie są gdy 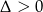 (czyli
(czyli 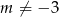 i
i 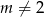 ) i
) i
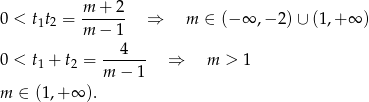
Zatem wszystko wiemy. Funkcja ilości pierwiastków wyraża się wzorem
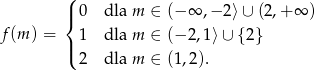
Teraz bez trudu szkicujemy wykres.
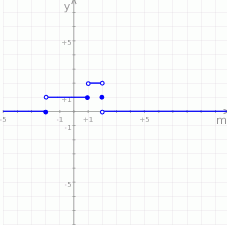
Odpowiedź: