/Szkoła średnia/Równania/Wykładnicze/Z parametrem

Zadanie nr 6301038

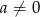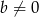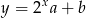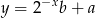Jaki warunek muszą spełniać liczby rzeczywiste a ⁄= 0 i b ⁄= 0 , aby wykresy funkcji y = 2xa + b i y = 2−xb + a miały dokładnie jeden punkt wspólny.

Wersja PDF

Rozwiązanie

Musimy ustalić kiedy równanie

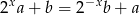
x −x 2 a+ b = 2 b + a

ma dokładnie jedno rozwiązanie. Podstawmy 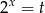x 2 = t . Mamy wtedy

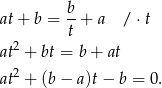
b at+ b = --+ a /⋅ t t at2 + bt = b+ at 2 at + (b − a)t − b = 0 .

Musimy sprawdzić kiedy to równanie ma dokładnie jeden pierwiastek dodatni (bo 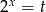2x = t daje wtedy dokładnie jednego x -a).

Z założenia 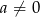a ⁄= 0 , czyli jest to równanie kwadratowe. Sprawdźmy teraz kiedy równanie ma pierwiastki.

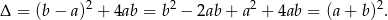
Δ = (b − a)2 + 4ab = b2 − 2ab + a2 + 4ab = (a+ b)2.

Zatem równanie ma zawsze pierwiastki, dwa jeżeli 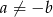a ⁄= −b . Jeżeli 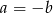a = −b to mamy równanie

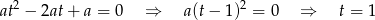
2 2 at − 2at+ a = 0 ⇒ a(t − 1) = 0 ⇒ t = 1

i jest OK.

Jeżeli 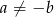a ⁄= −b to równanie kwadratowe ma dwa pierwiastki, musimy ustalić kiedy dokładnie jeden z nich jest dodatni. Ponieważ 0 nie jest pierwiastkiem (sprawdzamy wstawiając do równania), tak będzie jeżeli pierwiastki będą różnych znaków, czyli 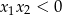x1x2 < 0 . Na mocy wzorów Viète’a daje to nam warunek:

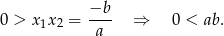
0 > x x = −b-- ⇒ 0 < ab . 1 2 a

 
Odpowiedź: 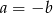a = −b lub ab > 0

Wersja PDF