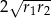Zadanie nr 5906819
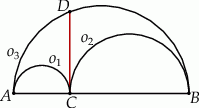
Na średnicy 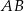 półokręgu
półokręgu 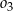 wybrano punkt
wybrano punkt 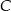 i na odcinkach
i na odcinkach 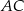 i
i 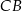 jako na średnicach skonstruowano półokręgi
jako na średnicach skonstruowano półokręgi 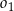 i
i 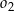 . Odcinek
. Odcinek 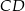 jest odcinkiem wspólnej stycznej półokręgów
jest odcinkiem wspólnej stycznej półokręgów 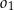 i
i 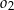 . Oblicz długość odcinka
. Oblicz długość odcinka 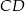 jeżeli promienie półokręgów
jeżeli promienie półokręgów 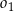 i
i 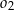 są odpowiednio równe
są odpowiednio równe 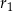 i
i 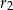 .
.
Rozwiązanie
Dorysujmy odcinki 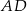 i
i 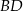 .
.
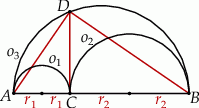
Wiemy, że 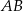 jest średnicą okręgu
jest średnicą okręgu 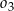 , więc trójkąt
, więc trójkąt 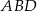 jest prostokątny. Prosta
jest prostokątny. Prosta 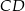 jako styczna do
jako styczna do 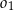 i
i 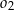 jest prostopadła do prostej łączącej środki tych okręgów, czyli do
jest prostopadła do prostej łączącej środki tych okręgów, czyli do 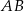 . W takim razie
. W takim razie 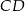 jest wysokością w trójkącie
jest wysokością w trójkącie 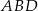 .
.
Aby obliczyć długość odcinka 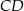 zauważmy, że trójkąty
zauważmy, że trójkąty 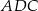 i
i 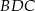 są podobne (bo każdy z nich jest podobny do trójkąta
są podobne (bo każdy z nich jest podobny do trójkąta  ). W takim razie
). W takim razie
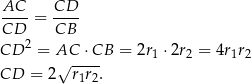
Odpowiedź: