/Szkoła podstawowa/Geometria/Czworokąty/Kwadrat

Zadanie nr 4813687

Dodaj do ulubionych
Dodaj do rozwiązanych

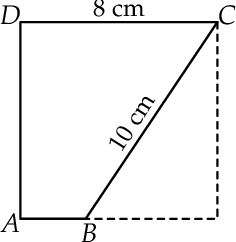
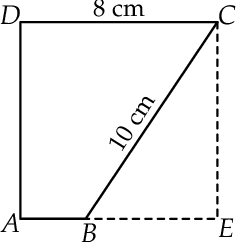
Z kwadratu o boku długości 8 cm wycięto trójkąt prostokątny o przeciwprostokątnej długości 10 cm w sposób pokazany na rysunku. Oblicz pole otrzymanego czworokąta 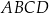ABCD .

ZINFO-FIGURE

Rozwiązanie

Z twierdzenia Pitagorasa obliczamy długość odcinka 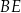BE .

ZINFO-FIGURE

Mamy

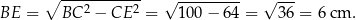
∘ ----------- √ --------- √ --- BE = BC 2 − CE 2 = 100 − 64 = 36 = 6 cm .

Sposób I

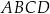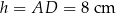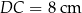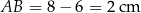Czworokąt ABCD jest trapezem prostokątnym o wysokości h = AD = 8 cm i podstawach długości DC = 8 cm i AB = 8 − 6 = 2 cm . Jego pole jest więc równe

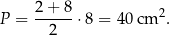
P = 2-+-8-⋅8 = 40 cm 2. 2

Sposób II

Pole czworokąta 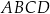ABCD możemy obliczyć odejmując od pola kwadratu o boku 8 cm, pole trójkąt prostokątnego 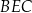BEC . Pole to jest więc równe

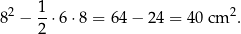
8 2 − 1⋅6 ⋅8 = 64− 24 = 40 cm 2. 2

 
Odpowiedź: 40 cm 2

Wersja PDF