/Szkoła podstawowa/Geometria/Trójkąt/Dowolny/Długości odcinków

Zadanie nr 2813451

Dwa spośród boków trójkąta mają długości 3 i 5. Zaznacz na osi liczbowej wszystkie liczby oznaczające możliwe długości trzeciego boku.

Wersja PDF

Rozwiązanie

Z trzech odcinków o długościach 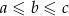a ≤ b ≤ c można zbudować trójkąt wtedy i tylko wtedy, gdy 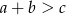a+ b > c (najdłuższy bok musi być krótszy od sumy długości dwóch pozostałych boków).

Niech x oznacza długość trzeciego boku trójkąta, w którym dwa boki mają długości 3 i 5. Możliwe są dwie sytuacje.

Jeżeli najdłuższym bokiem trójkąta jest bok długości x , to musi być spełniony warunek

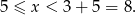
5 ≤ x < 3 + 5 = 8.

Jeżeli natomiast najdłuższym bokiem trójkąta jest bok długości 5, to musi być spełniony warunek

x + 3 > 5 oraz x ≤ 5 x > 2 oraz x ≤ 5 2 < x ≤ 5.

Łącząc nierówności otrzymane w obu przypadkach otrzymujemy nierówność

2 < x < 8 .

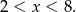
Zaznaczamy teraz ten zbiór na osi liczbowej.

PIC

Wersja PDF