/Szkoła podstawowa/Geometria/Trójkąt/Dowolny/Długości odcinków

Zadanie nr 6291755

Ile jest trójkątów o obwodzie równym 19, w których długości boków wyrażone są liczbami całkowitymi. Wymień je.

Wersja PDF

Rozwiązanie

Długości 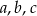a,b,c boków trójkąta muszą spełniać nierówności trójkąta

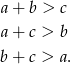
a + b > c a + c > b b + c > a.

Zatem najdłuższy bok trójkąta musi być równy co najwyżej 9 (bo suma dwóch pozostałych ma być większa). Mamy następujące trójkąty z najdłuższym bokiem 9:

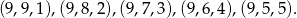
(9,9,1),(9,8,2),(9,7,3),(9,6,4 ),(9,5,5).

Jeżeli najdłuższy bok jest równy 8, to mamy trójkąty

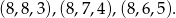
(8,8,3),(8,7,4),(8,6,5 ).

Jeżeli najdłuższy bok jest równy 7, to mamy trójkąty

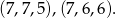
(7,7,5),(7,6,6).

I to koniec, bo gdyby najdłuższy bok był równy 6, to obwód jest nie większy od 18.  
Odpowiedź: 10 trójkątów

Wersja PDF