Zadanie nr 1485869
Sinus kąta 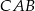 trójkąta równoramiennego
trójkąta równoramiennego 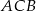 jest równy
jest równy 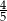 . Pole kwadratu
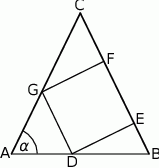
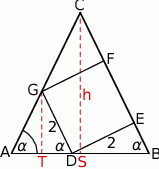
. Pole kwadratu 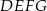 , wpisanego w ten trójkąt (zobacz rysunek), jest równe 4. Oblicz pole trójkąta
, wpisanego w ten trójkąt (zobacz rysunek), jest równe 4. Oblicz pole trójkąta 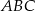 .
.
Rozwiązanie
Oczywiście bok kwadratu 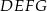 to 2. Zauważmy, że
to 2. Zauważmy, że  jest równoramienny (bo
jest równoramienny (bo 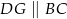 ).
).
Niech 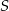 i
i 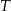 będą środkami odpowiednio odcinków
będą środkami odpowiednio odcinków 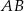 i
i 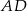 . Patrzymy teraz na trójkąty prostokątne
. Patrzymy teraz na trójkąty prostokątne 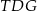 i
i 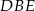 .
.
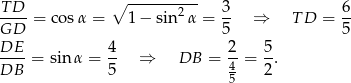
W takim razie
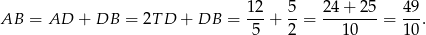
Brakuje nam jeszcze wysokości trójkąta 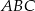 – aby ją obliczyć patrzymy na trójkąt prostokątny
– aby ją obliczyć patrzymy na trójkąt prostokątny 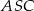 .
.
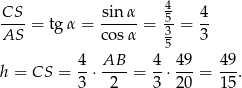
Pole trójkąta 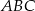 jest więc równe
jest więc równe
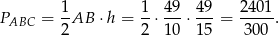
Odpowiedź: