/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny/Pole

Zadanie nr 2257587

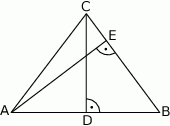
Oblicz pole trójkąta równoramiennego 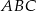ABC (patrz rysunek, 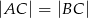|AC | = |BC | ), w którym wysokość 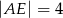|AE | = 4 , a długość odcinka |BE | = 3 .

PIC

Wersja PDF

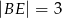Rozwiązanie

Korzystając z twierdzenia Pitagorasa w trójkącie 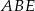ABE obliczmy długość podstawy trójkąta ABC .

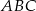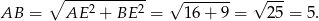
∘ ----------- √ ------- √ --- AB = AE 2 + BE 2 = 16 + 9 = 25 = 5.

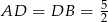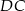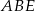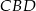W takim razie AD = DB = 52 . Wysokość DC obliczamy korzystając z podobieństwa trójkątów ABE i CBD (oba są prostokątne i mają wspólny kąt przy wierzchołku B ).

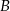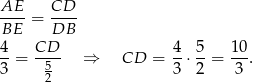
AE-- CD-- BE = DB 4 CD 4 5 10 --= -5-- ⇒ CD = --⋅ --= ---. 3 2 3 2 3

Pole trójkąta 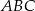ABC jest więc równe

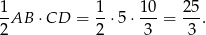
1AB ⋅CD = 1-⋅5 ⋅ 10-= 25-. 2 2 3 3

 
Odpowiedź: 253

Wersja PDF