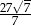/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny/Pole

Zadanie nr 8240295

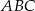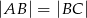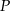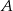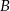W trójkącie równoramiennym ABC , gdzie |AB | = |BC | , podstawa ma długość 6. Punkt P jest punktem przecięcia wysokości wychodzących z wierzchołków A i B . Oblicz pole tego trójkąta, jeśli |CP | = 4 .

Wersja PDF

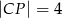Rozwiązanie

Rozpoczynamy od rysunku.

PIC

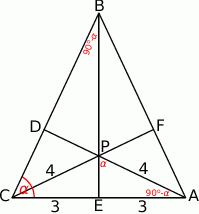
Ponieważ wysokości trójkąta przecinają się w jednym punkcie, odcinek 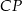CP jest fragmentem wysokości opuszczonej z wierzchołka 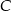C . Stosując twierdzenie Pitagorasa w trójkącie 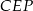CEP mamy

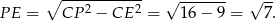
∘ ----------- √ ------- √ -- P E = CP 2 − CE 2 = 16− 9 = 7.

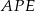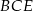Teraz kluczowa obserwacja: trójkąty AP E i BCE są podobne. Rzeczywiście, jeżeli oznaczymy 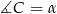∡C = α to w trójkącie prostokątnym 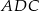ADC mamy

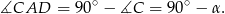
∘ ∘ ∡CAD = 90 − ∡C = 9 0 − α.

Zatem z trójkąta prostokątnego 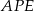AP E

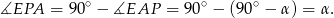
∘ ∘ ∘ ∡EPA = 90 − ∡EAP = 90 − (9 0 − α) = α.

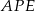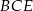W takim razie trójkąty AP E i BCE są oba prostokątne i oba mają kąt o mierze α , są więc podobne.

Dzięki temu podobieństwu możemy obliczyć długość wysokości 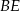BE .

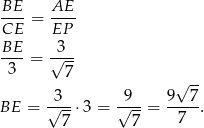
BE AE ----= ---- CE EP BE- = √3-- 3 7 √ -- BE = √3--⋅3 = √9--= 9--7. 7 7 7

Pozostało obliczyć pole trójkąta 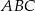ABC .

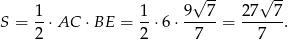
√ -- √ -- 1- 1- 9---7 27---7 S = 2 ⋅AC ⋅BE = 2 ⋅6 ⋅ 7 = 7 .

 
Odpowiedź: √ - 27--7 7

Wersja PDF