Zadanie nr 1552465
Punkt 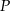 , będący punktem wewnętrznym trójkąta
, będący punktem wewnętrznym trójkąta 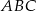 , przekształcamy przez symetrię względem prostych zawierających boki
, przekształcamy przez symetrię względem prostych zawierających boki 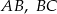 i
i 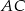 otrzymując odpowiednio punkty
otrzymując odpowiednio punkty 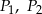 i
i 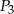 . Udowodnij, że pole sześciokąta
. Udowodnij, że pole sześciokąta 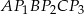 jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta 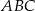 .
.
Rozwiązanie
Zaczynamy od rysunku.
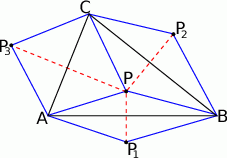
Teza zadania wynika natychmiast z obserwacji, że trójkąty 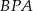 i
i 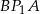 ,
, 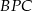 i
i 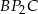 oraz
oraz 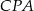 i
i 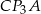 są przystające.
są przystające.

