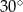Zadanie nr 8343106
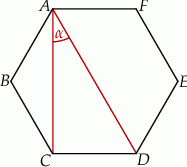
Oblicz miarę kąta  jaki tworzą przekątne
jaki tworzą przekątne 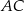 i
i 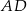 sześciokąta foremnego.
sześciokąta foremnego.
Rozwiązanie
Miarę kąta  można wyliczyć na wiele różnych sposobów.
można wyliczyć na wiele różnych sposobów.
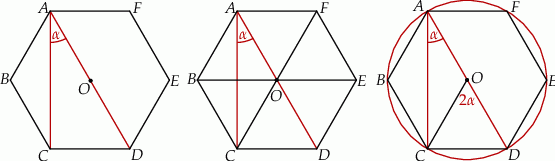
Sposób I
Przekątna 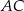 jest prostopadła do
jest prostopadła do 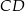 , czyli
, czyli 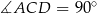 . Przekątna
. Przekątna 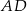 jest natomiast dwusieczną kąta
jest natomiast dwusieczną kąta 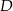 , którego miara wynosi
, którego miara wynosi 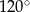 . Zatem
. Zatem 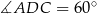 . Mamy stąd
. Mamy stąd
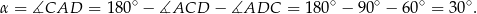
Sposób II
Jeżeli połączymy środek sześciokąta z jego wierzchołkami to otrzymamy 6 trójkątów równobocznych. Widać teraz, że szukany kąt jest równy kątowi jaki tworzy wysokość w trójkącie równobocznym z jego bokiem. Jest to więc 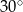 .
.
Sposób III
Jeżeli dorysujemy okrąg opisany na sześciokącie foremnym, to kąt środkowy 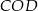 jest oparty na tym samym łuku, co szukany kąt
jest oparty na tym samym łuku, co szukany kąt 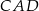 . Zatem
. Zatem
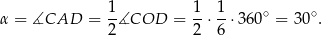
Odpowiedź: