/Szkoła średnia/Nierówności/Udowodnij.../Trygonometryczne

Zadanie nr 5687507

Dodaj do ulubionych
Dodaj do rozwiązanych

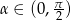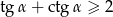Wykaż, że dla każdej liczby π- α ∈ (0,2 ) zachodzi nierówność tgα + ctg α ≥ 2 .

Rozwiązanie

Sposób I

Przekształćmy podaną nierówność

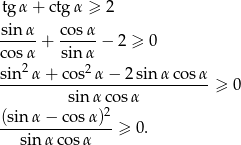
tgα + ctg α ≥ 2 sin-α- cosα- cosα + sinα − 2 ≥ 0 sin 2α + cos2 α− 2sinα cos α -----------------------------≥ 0 sinα cos α (sin-α-−-cos-α)2- sin αco sα ≥ 0.

Teraz wystarczy zauważyć, że dzięki założeniu 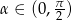α ∈ (0 , π) 2 mianownik jest dodatni. Licznik jest nieujemny, więc powyższa nierówność jest prawdziwa.

Sposób II

Tym razem zamieńmy cotangens na tangens.

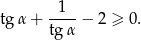
-1-- tg α+ tgα − 2 ≥ 0.

Z założenia 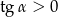tg α > 0 , więc możemy przez niego pomnożyć stronami.

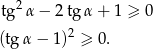
tg 2α − 2 tg α + 1 ≥ 0 2 (tg α− 1) ≥ 0.

Otrzymana nierówność jest oczywiście zawsze spełniona.

Wersja PDF