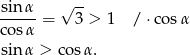Zadanie nr 7017932
Wykaż, że jeżeli  jest kątem ostrym spełniającym warunek
jest kątem ostrym spełniającym warunek 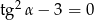 to
to 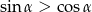 .
.
Rozwiązanie
Przekształcamy daną równość
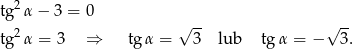
Ponieważ  jest kątem ostrym, więc
jest kątem ostrym, więc 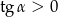 . Zatem
. Zatem
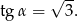
Zauważmy, że 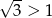 . Wówczas z tożsamości
. Wówczas z tożsamości 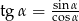 otrzymujemy
otrzymujemy
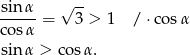
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że jeżeli  jest kątem ostrym spełniającym warunek
jest kątem ostrym spełniającym warunek 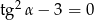 to
to 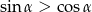 .
.
Przekształcamy daną równość
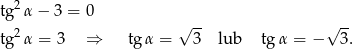
Ponieważ  jest kątem ostrym, więc
jest kątem ostrym, więc 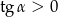 . Zatem
. Zatem
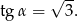
Zauważmy, że 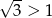 . Wówczas z tożsamości
. Wówczas z tożsamości 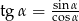 otrzymujemy
otrzymujemy