Zadanie nr 3273105
Wyznacz te wartości parametru 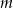 , dla których równanie
, dla których równanie
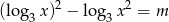
ma dwa rozwiązania należące do przedziału 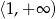 .
.
Rozwiązanie
Oczywiście ze względu na dziedzinę logarytmu musi być 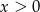 . Dane równanie możemy zapisać w postaci
. Dane równanie możemy zapisać w postaci
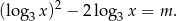
Jeżeli podstawimy teraz 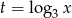 to mamy równanie kwadratowe
to mamy równanie kwadratowe
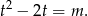
Sprawa jest więc dość prosta, ale musimy być trochę ostrożni, bo musimy uwzględnić warunek 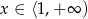 . Przy tym założeniu mamy
. Przy tym założeniu mamy 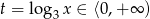 . Pytanie więc brzmi: dla jakich wartości parametru
. Pytanie więc brzmi: dla jakich wartości parametru 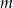 równanie
równanie
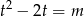
ma dwa rozwiązania nieujemne? Najłatwiej odpowiedzieć na to pytanie szkicując wykres lewej strony – jest to parabola o miejscach zerowych 0, 2 i wierzchołku w punkcie 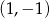 .
.
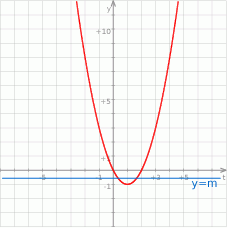
Widać teraz, że powyższe równanie kwadratowe ma dwa pierwiastki nieujemne dla 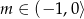
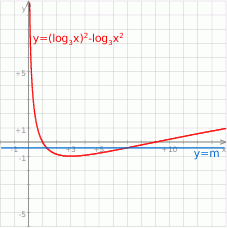
Na koniec (dla ciekawskich) wykres lewej strony oryginalnego równania, czyli funkcji 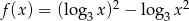 .
.
Odpowiedź: