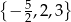/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą/Przez stopnia 1

Zadanie nr 4088217

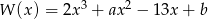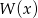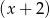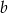Dany jest wielomian 3 2 W (x) = 2x + ax − 13x+ b . Liczba 3 jest jednym z pierwiastków tego wielomianu. Reszta z dzielenia wielomianu W (x ) przez (x + 2) jest równa 20. Oblicz współczynniki a i b oraz pozostałe pierwiastki wielomianu W (x) .

Wersja PDF

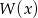Rozwiązanie

Reszta z dzielenia wielomianu 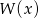W (x) przez jednomian 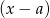(x − a) to po prostu 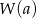W (a) – aby to sprawdzić, wystarczy podstawić 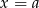x = a w równości

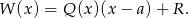
W (x ) = Q (x)(x− a)+ R.

Więcej szczegółów znajdziecie w poradniku o wielomianach.

Mamy zatem układ równań

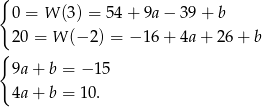
{ 0 = W (3) = 54+ 9a− 39 + b 20 = W (− 2 ) = − 16+ 4a+ 26+ b { 9a+ b = − 15 4a+ b = 10.

Odejmujemy te równania stronami (żeby skrócić 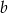b ) i mamy

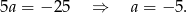
5a = −2 5 ⇒ a = − 5.

Stąd 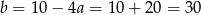b = 10 − 4a = 10+ 20 = 30 i

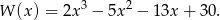
W (x) = 2x3 − 5x2 − 13x + 30.

Dzielimy teraz powyższy wielomian przez 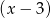(x − 3) . My zrobimy to grupując wyrazy.

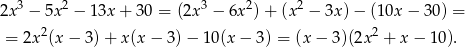
3 2 3 2 2 2x − 5x − 1 3x+ 30 = (2x − 6x )+ (x − 3x )− (10x − 30) = = 2x 2(x− 3)+ x(x − 3)− 10(x − 3) = (x − 3)(2x2 + x− 10).

Rozkładamy teraz trójmian w drugim nawiasie.

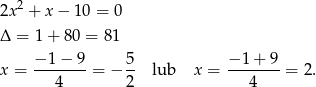
2 2x + x− 10 = 0 Δ = 1 + 80 = 81 x = −-1-−-9 = − 5- lub x = −-1-+-9 = 2. 4 2 4

 
Odpowiedź: 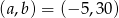(a,b) = (− 5,3 0) , pierwiastki: { } − 5,2,3 2

Wersja PDF