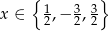/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą/Przez stopnia 1

Zadanie nr 5744913

Przy dzieleniu wielomianu 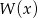W (x ) przez dwumian 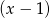(x − 1) otrzymujemy iloraz 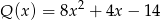Q (x) = 8x2 + 4x − 14 oraz resztę 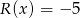R (x) = − 5 . Oblicz pierwiastki wielomianu W (x) .

Wersja PDF

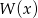Rozwiązanie

Z podanych informacji wiemy, że

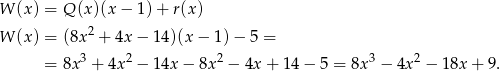
W (x) = Q (x )(x − 1)+ r(x ) W (x) = (8x 2 + 4x− 14)(x − 1) − 5 = 3 2 2 3 2 = 8x + 4x − 14x − 8x − 4x + 1 4− 5 = 8x − 4x − 18x + 9 .

Pozostało zatem rozwiązać równanie (od razu wielomian dzielimy przez 2)

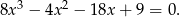
3 2 8x − 4x − 18x + 9 = 0.

Można teraz szukać pierwiastków wymiernych, ale jest to kłopotliwe rachunkowo, bo tak się składa, że to równanie nie ma pierwiastków całkowitych i pierwszy pierwiastek jaki mamy szanse znaleźć to 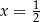x = 12 . Zamiast tego, można jednak łatwo zauważyć rozkład tego wielomianu grupując czynniki.

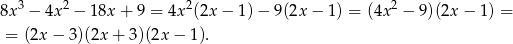
8x3 − 4x2 − 18x + 9 = 4x2(2x − 1 )− 9(2x − 1) = (4x2 − 9)(2x − 1 ) = = (2x − 3)(2x + 3)(2x− 1).

Zatem pierwiastki to 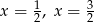x = 1, x = 3 2 2 oraz x = − 3 2 .  
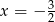Odpowiedź: { } x ∈ 12,− 32, 32

Wersja PDF