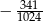/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą/Przez stopnia 1

Zadanie nr 5962296

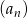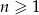Niech ciąg (an) , dla n ≥ 1 , będzie resztą z dzielenia wielomianu 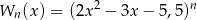Wn (x ) = (2x2 − 3x − 5,5)n przez dwumian 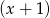(x+ 1) . Oblicz sumę dziesięciu początkowych wyrazów ciągu (an) .

Wersja PDF

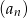Rozwiązanie

Ponieważ reszta z dzielenia wielomianu 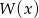W (x ) przez dwumian 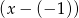(x− (− 1)) jest równa 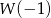W (− 1) . Mamy

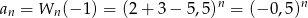
an = Wn (− 1) = (2+ 3 − 5 ,5)n = (− 0,5)n

Jest to więc ciąg geometryczny o pierwszym wyrazie 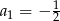a1 = − 12 i ilorazie 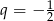q = − 1 2 . Suma 10 początkowych wyrazów ego ciągu jest równa

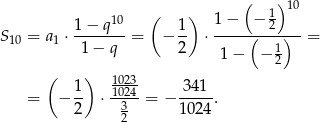
( ) ( 1)10 1-−-q10 1- 1-−---−-2--- S10 = a1 ⋅ 1 − q = − 2 ⋅ ( 1) = 1 − − 2 ( ) 1023 = − 1- ⋅1024 = − 341-. 2 3 1024 2

 
Odpowiedź: − -341- 1024

Wersja PDF