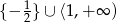Zadanie nr 6176699
Reszta z dzielenia wielomianu 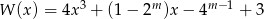 przez dwumian
przez dwumian 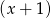 jest równa -2.
jest równa -2.
- Wyznacz wartość parametru
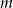 .
. - Dla wyznaczonej wartości parametru
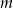 rozwiąż nierówność
rozwiąż nierówność 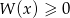 .
.
Rozwiązanie
- Reszta z dzielenia wielomianu
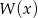 przez dwumian
przez dwumian 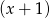 to po prostu
to po prostu 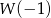 , co daje nam równanie
, co daje nam równanie 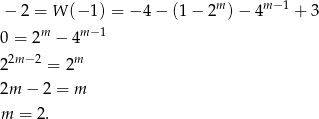
Odpowiedź: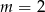
- Podstawiamy
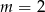 i otrzymujemy nierówność
i otrzymujemy nierówność 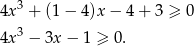
Widać gołym okiem, że
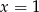 jest pierwiastkiem wielomianu, więc dzielimy go przez
jest pierwiastkiem wielomianu, więc dzielimy go przez 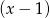 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy. 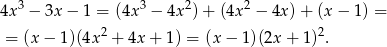
Mamy zatem nierówność
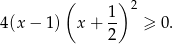
Jej rozwiązaniem jest zbiór
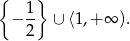
Odpowiedź: