/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą/Przez stopnia 1

Zadanie nr 7631843

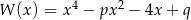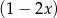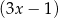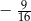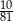Reszty z dzielenia wielomianu 4 2 W (x) = x − px − 4x + q przez dwumiany (1 − 2x ) i (3x− 1) są odpowiednio równe − 196 i 1081- . Oblicz resztę z dzielenia wielomianu 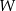W przez dwumian (3 − 2x ) .

Wersja PDF

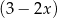Rozwiązanie

Reszta z dzielenia wielomianu 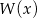W (x) przez dwumian 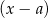(x − a) lub przez dwumian 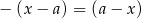− (x − a ) = (a− x) to po prostu 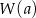W (a) (aby to zauważyć wystarczy w równości 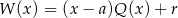W (x ) = (x − a)Q (x) + r lub w równości 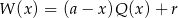W (x) = (a− x )Q (x)+ r podstawić x = a ). Mamy zatem układ równań

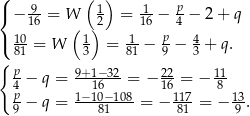
( ( ) { − 9-= W 1 = 1-− p − 2 + q 16 ( )2 16 4 ( 10= W 1 = -1 − p − 4 + q. { 81 3 81 9 3 p− q = 9+1−-32= − 22 = − 11 4p 1−1160−-108- 16117- 8 13 9 − q = 81 = − 81 = − 9 .

Odejmujemy od pierwszego równania drugie i mamy

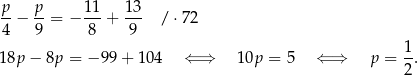
p-− p-= − 11-+ 1-3 / ⋅72 4 9 8 9 1- 18p − 8p = − 99 + 104 ⇐ ⇒ 10p = 5 ⇐ ⇒ p = 2.

Stąd

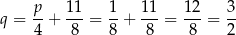
p- 11- 1- 11- 12- 3- q = 4 + 8 = 8 + 8 = 8 = 2

i

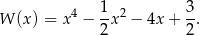
1 3 W (x ) = x4 − -x 2 − 4x + -. 2 2

Reszta z dzielenia tego wielomianu przez dwumian 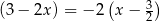(3− 2x) = − 2 (x− 3) 2 jest równa

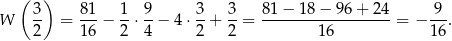
( 3 ) 81 1 9 3 3 81 − 18 − 96 + 24 9 W -- = ---− --⋅ -− 4⋅ --+ --= ------------------= − ---. 2 16 2 4 2 2 16 16

 
Odpowiedź: -9 − 16

Wersja PDF