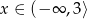/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą/Przez stopnia 1

Zadanie nr 7855250

Dany jest wielomian 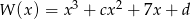3 2 W (x) = x + cx + 7x + d .

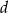  • Wyznacz wartości współczynników c i d wielomianu 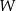W , wiedząc, że jest podzielny przez dwumian 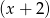(x+ 2) , zaś przy dzieleniu przez dwumian 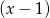(x − 1) otrzymujemy resztę 3.
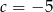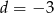  • Dla c = − 5 i d = −3 rozwiąż nierówność W (x) ≤ 0 .
Wersja PDF

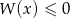Rozwiązanie

  • Jeżeli wielomian dzieli się przez 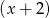(x + 2 ) to dla 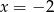x = − 2 musi przyjmować wartość 0 (bo tę własność ma 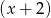(x + 2) ). Zatem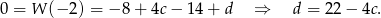
    0 = W (− 2) = − 8 + 4c − 14 + d ⇒ d = 22 − 4c.

    Jeżeli natomiast reszta z dzielenia przez dwumian 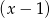(x − 1) wynosi 3, to musi być 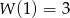W (1) = 3 (aby w to uwierzyć wystarczy sobie napisać równość 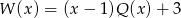W (x) = (x − 1)Q (x )+ 3 i podstawić w niej 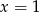x = 1 ). Mamy zatem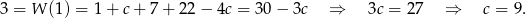

    3 = W (1) = 1 + c + 7 + 22 − 4c = 30− 3c ⇒ 3c = 27 ⇒ c = 9.

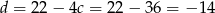    Zatem d = 22 − 4c = 22 − 3 6 = − 14 .  
    Odpowiedź: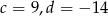 c = 9,d = − 14

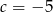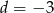  • Dla c = − 5 i d = −3 mamy wielomian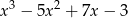
    x3 − 5x2 + 7x − 3

    Od razu spróbujmy go rozłożyć. Sprawdzając dzielniki wyrazu wolnego znajdujemy pierwiastek 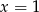x = 1 . Dzielimy więc wielomian przez 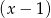(x − 1) – my zrobimy to grupując wyrazy.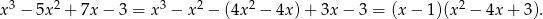

    x 3 − 5x 2 + 7x− 3 = x3 − x2 − (4x2 − 4x) + 3x − 3 = (x− 1)(x2 − 4x + 3).

    Rozkładamy teraz otrzymany trójmian.

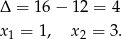
    Δ = 16 − 12 = 4 x1 = 1, x2 = 3.

    Mamy więc do rozwiązania nierówność

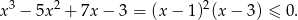
    3 2 2 x − 5x + 7x − 3 = (x − 1) (x − 3) ≤ 0.

    Jej rozwiązaniem jest zbiór (− ∞ ,3⟩ .  
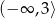    Odpowiedź: x ∈ (− ∞ ,3⟩

Wersja PDF