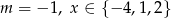Zadanie nr 8571068
Reszty z dzielenia wielomianu 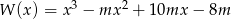 przez dwumiany
przez dwumiany 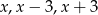 są kolejnymi wyrazami ciągu arytmetycznego. Oblicz wartość parametru
są kolejnymi wyrazami ciągu arytmetycznego. Oblicz wartość parametru 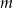 oraz pierwiastki tego wielomianu.
oraz pierwiastki tego wielomianu.
Rozwiązanie
Reszta z dzielenia wielomianu 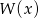 przez dwumian
przez dwumian 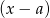 to po prostu
to po prostu 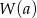 , więc mamy równanie
, więc mamy równanie
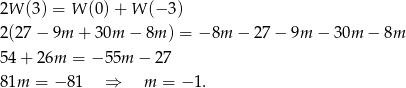
Pozostało rozwiązać równanie
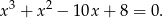
Szukamy najpierw rozwiązań całkowitych sprawdzając dzielniki wyrazu wolnego. Łatwo sprawdzić, że jednym z pierwiastków jest 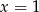 . Dzielimy więc lewą stronę równania przez
. Dzielimy więc lewą stronę równania przez 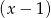 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
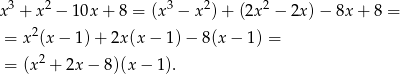
Teraz rozkładamy trójmian w pierwszym nawiasie.
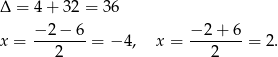
Zatem równanie ma trzy rozwiązania: 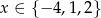 .
.
Odpowiedź: