/Szkoła średnia/Liczby/Liczby całkowite/Różne

Zadanie nr 9749571

Dodaj do ulubionych
Dodaj do rozwiązanych

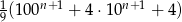Udowodnij, że dla każdej liczby naturalnej n , liczba 1 n+1 n+1 9(10 0 + 4 ⋅10 + 4) jest kwadratem liczby naturalnej.

Rozwiązanie

Korzystamy ze wzoru skróconego mnożenia

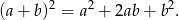
2 2 2 (a+ b ) = a + 2ab+ b .

Liczymy

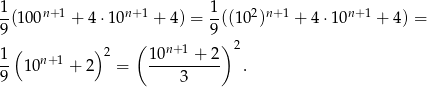
1 1 -(10 0n+1 + 4⋅ 10n+1 + 4) = -((102)n+ 1 + 4 ⋅10n+ 1 + 4) = 9 9 1 ( )2 ( 10n +1 + 2) 2 -- 10n+ 1 + 2 = ---------- . 9 3

No i mamy kwadrat, ale to jeszcze nie koniec, bo musimy wiedzieć, że liczba w nawiasie jest naturalna. Aby to uzasadnić musimy pokazać, że 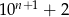10n +1 + 2 dzieli się przez 3. Najłatwiej to zrobić patrząc na sumę cyfr: jest równa 3 (bo ta liczba ma pierwszą cyfrę równą 1, ostatnią równą 2, a wszystkie pozostałe równe 0).

Wersja PDF