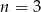Zadanie nr 8902934
Wyznacz wszystkie liczby naturalne  , dla których
, dla których 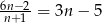 .
.
Rozwiązanie
Przekształcamy dane równanie.
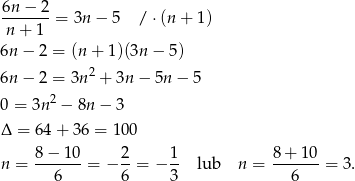
Jedynym rozwiązaniem naturalnym danego równania jest więc 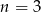 .
.
Odpowiedź: 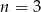
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wyznacz wszystkie liczby naturalne  , dla których
, dla których 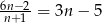 .
.
Przekształcamy dane równanie.
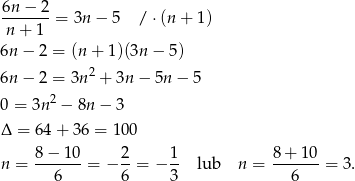
Jedynym rozwiązaniem naturalnym danego równania jest więc 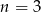 .
.
Odpowiedź: