Zadanie nr 7799106
Niech  będzie liczbą naturalną, a
będzie liczbą naturalną, a  i
i 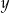 dodatnimi liczbami rzeczywistymi takimi, że
dodatnimi liczbami rzeczywistymi takimi, że 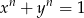 . Udowodnij nierówność:
. Udowodnij nierówność:
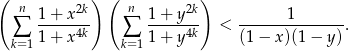
Rozwiązanie
Sposób I
Zaczniemy od lematu.
Lemat
Dla dowolnego 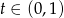 zachodzi nierówność
zachodzi nierówność
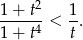
Dowód Wymnażając stronami dostajemy nierówność
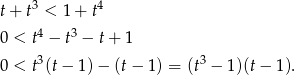
Ponieważ oba nawiasy są ujemne, nierówność jest spełniona.
Z powyższej nierówności mamy (dla 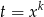 )
)
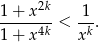
Stąd
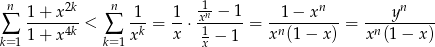
Podobnie
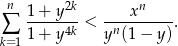
Zatem
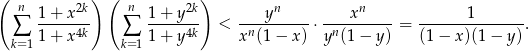
Sposób II
Skorzystamy z tzw. nierówności Karamaty
Twierdzenie
Niech 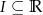 będzie przedziałem na prostej. Jeżeli dane są liczby
będzie przedziałem na prostej. Jeżeli dane są liczby 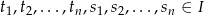 takie, że
takie, że
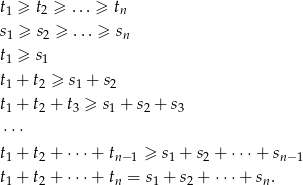
oraz funkcja wypukła 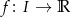 to
to
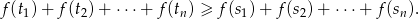
Zaczniemy od lematu.
Lemat
Jeżeli 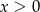 , to dla dowolnego
, to dla dowolnego 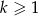
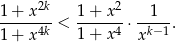
Dowód Wymnóżmy powyższą nierówność
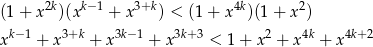
Aby uzasadnić tę nierówność wystarczy skorzystać z nierówności Karamaty dla funkcji 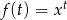 i ciągów
i ciągów
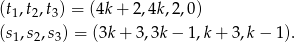
Mamy zatem
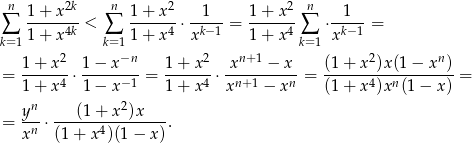
Podobnie
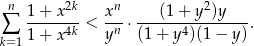
Zatem nierówność, którą mamy udowodnić możemy zapisać w postaci
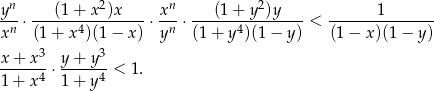
Tę nierówność łatwo uzasadnić, ponownie korzystając z nierówności Karamaty
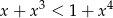
(dla ciągów 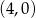 i
i 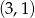 ).
).

