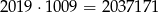Zadanie nr 4397428
Oblicz
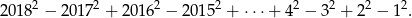
Rozwiązanie
Korzystamy ze wzoru na różnicę kwadratów.
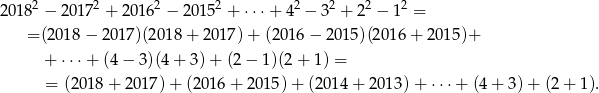
Otrzymane wyrażenie to suma 2018 początkowych wyrazów ciągu arytmetycznego 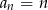 . Jest ona równa
. Jest ona równa
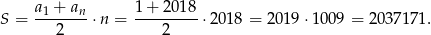
Odpowiedź: 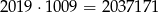
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz
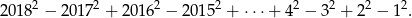
Korzystamy ze wzoru na różnicę kwadratów.
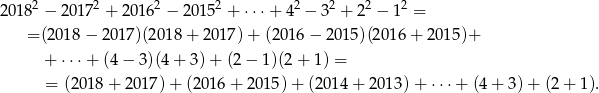
Otrzymane wyrażenie to suma 2018 początkowych wyrazów ciągu arytmetycznego 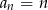 . Jest ona równa
. Jest ona równa
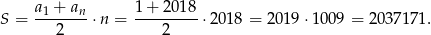
Odpowiedź: