/Konkursy/Zadania/Geometria/Planimetria/Prostokąt/Różne

Zadanie nr 1787847

Dodaj do ulubionych
Dodaj do rozwiązanych

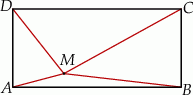
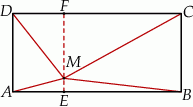
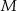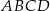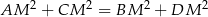Punkt M leży wewnątrz prostokąta ABCD (zob. rysunek). Udowodnij, że AM 2 + CM 2 = BM 2 + DM 2 .

PIC

Rozwiązanie

Sposób I

Dorysujmy dwa pionowe odcinki 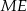ME i MF .

PIC

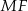Mamy wtedy

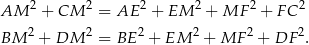
2 2 2 2 2 2 AM + CM = AE + EM + MF + FC BM 2 + DM 2 = BE 2 + EM 2 + MF 2 + DF 2.

Aby zobaczyć, że wyrażenia te są identyczne, wystarczy zauważyć, że 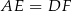AE = DF i FC = BE .

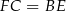Sposób II

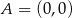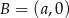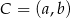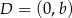Możemy prostokąt umieścić w układzie współrzędnych tak, aby A = (0,0) , B = (a,0) , C = (a,b) i D = (0 ,b ) . Jeżeli oznaczymy 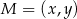M = (x,y) to mamy

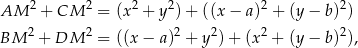
2 2 2 2 2 2 AM + CM = (x + y ) + ((x − a) + (y − b) ) BM 2 + DM 2 = ((x − a)2 + y2) + (x2 + (y − b)2),

co kończy dowód. Z tego rozwiązania widać wyraźnie, że nie jest istotne, iż punkt 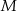M jest wewnątrz prostokąta.

Wersja PDF