/Szkoła średnia/Zadania maturalne/Matura 2009/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 18 kwietnia 2009 Czas pracy: 120 minut
Punkty 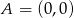 i
i 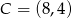 są wierzchołkami rombu
są wierzchołkami rombu 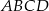 , którego jeden z boków zawiera się w prostej
, którego jeden z boków zawiera się w prostej 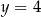 . Wyznacz współrzędne pozostałych wierzchołków rombu.
. Wyznacz współrzędne pozostałych wierzchołków rombu.
Rozwiąż równanie 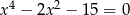 .
.
Korzystając z danych przedstawionych na rysunku oblicz wartość wyrażenia
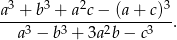
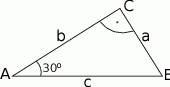
W poniższej tabeli przedstawiono obowiązującą w 2009 roku skale podatkową podatku PIT.
| Podstawa obliczenia podatku w pełnych złotych | Podatek wynosi |
| do 3089 | 0zł |
| od 3090 zł do 44490 zł | 19% minus kwota 586,85 zł |
| od 44490 zł do 85528 zł | 7866,25 zł plus 30% nadwyżki ponad 44490 zł |
| od 85528 zł | 20177,65 zł plus 40% nadwyżki ponad 85528 zł |
Po wypełnieniu formularza podatkowego okazało się, że Pan Adam musi zapłacić 9889,45 zł podatku.
- Oblicz podstawę obliczenia podatku pana Adama.
- O ile procent wzrósłby należny podatek pana Adama, gdyby jego podstawa wzrosła o 100%? Wynik podaj z dokładnością do 1%.
Pewna parabola o wierzchołku 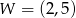 przecina oś
przecina oś 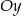 w punkcie
w punkcie 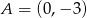 .
.
- Wyznacz postać ogólną funkcji kwadratowej
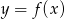 , której wykresem jest ta parabola.
, której wykresem jest ta parabola. - Rozwiąż nierówność
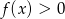 .
.
Wartość pewnej frezarki maleje z roku na rok. Wartości tej frezarki w kolejnych latach tworzą ciąg arytmetyczny. Oblicz czas, w ciągu którego frezarka całkowicie straci wartość (zamortyzuje się), jeżeli wiadomo, że po 15 latach użytkowania jej wartość była 3 razy większa niż jej wartość po 25 latach.
Rozwiąż równanie
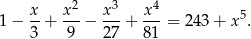
Dane są dwie bryły: stożek, w którym długość promienia podstawy jest równa 2 dm i wysokość ma długość 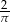 dm oraz ostrosłup prawidłowy trójkątny, w którym krawędź podstawy ma długość 4 dm. Wiedząc, że objętości tych brył są równe, wyznacz kąt nachylenia ściany bocznej ostrosłupa do jego podstawy.
dm oraz ostrosłup prawidłowy trójkątny, w którym krawędź podstawy ma długość 4 dm. Wiedząc, że objętości tych brył są równe, wyznacz kąt nachylenia ściany bocznej ostrosłupa do jego podstawy.
Rzucamy trzy razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania iloczynu oczek równego 12.
Funkcja 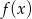 , gdzie
, gdzie 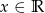 dana jest wzorem
dana jest wzorem
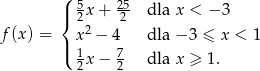
- Narysuj wykres funkcji
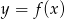 .
. - Odczytaj z wykresu rozwiązanie nierówności
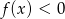 .
.
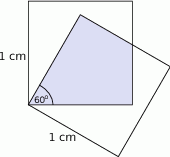
Kwadratowe szklane płytki o boku długości 1 cm, połączone w jednym wierzchołku, rozsunęły się tak, że boki wychodzące z jednego wierzchołka tworzą ze sobą kąt 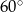 . Oblicz pole części wspólnej płytek. Wynik podaj z dokładnością do
. Oblicz pole części wspólnej płytek. Wynik podaj z dokładnością do 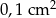 .
.
Wyznacz wymiary prostokąta o obwodzie 36 cm, którego pole jest największe.

