/Szkoła średnia/Zadania maturalne/Matura 2009/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 9 maja 2009 Czas pracy: 180 minut
W prostokącie, którego krótszy bok ma długość 8 zawarty jest kwadrat o boku równym różnicy
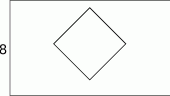
długości boków prostokąta, i którego przekątne są równoległe do boków prostokąta.
- Wyraź pole pozostałe po wycięciu kwadratu z prostokąta jako funkcję dłuższego boku prostokąta. Wyznacz dziedzinę otrzymanej funkcji.
- Wykaż, że różnica pól prostokąta i kwadratu jest zawsze większa od 64.
Uzasadnij, że suma kwadratów dwóch kolejnych nieparzystych liczb całkowitych nie może być kwadratem liczby całkowitej.
Współrzędne przeciwległych wierzchołków prostokąta  są równe
są równe 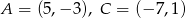 . Wyznacz współrzędne pozostałych wierzchołków prostokąta wiedząc, że wierzchołek
. Wyznacz współrzędne pozostałych wierzchołków prostokąta wiedząc, że wierzchołek 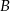 leży na prostej
leży na prostej 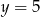 .
.
Wyznacz wszystkie rozwiązania równania 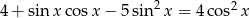 należące do przedziału
należące do przedziału 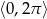 .
.
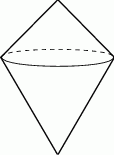
Boja ma kształt dwóch stożków połączonych podstawami, przy czym kąty rozwarcia tych stożków są równe 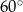 i
i 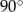 , a odległość ich wierzchołków jest równa
, a odległość ich wierzchołków jest równa 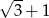 . Oblicz pole powierzchni tej boi.
. Oblicz pole powierzchni tej boi.
Wyznacz wszystkie wartości parametru 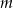 , dla których wielomian
, dla których wielomian
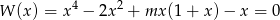
ma 4 różne pierwiastki.
Na bokach 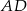 i
i 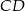 kwadratu
kwadratu 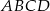 o boku długości 1 wybrano punkty
o boku długości 1 wybrano punkty 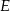 i
i 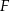 w ten sposób, że
w ten sposób, że 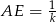 i
i 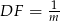 , dla
, dla 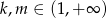 . Niech
. Niech 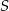 będzie punktem przecięcia odcinków
będzie punktem przecięcia odcinków 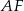 i
i 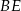
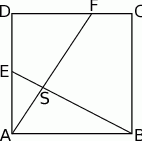
- Wykaż, że jeżeli trójkąt
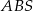 jest prostokątny to
jest prostokątny to 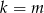 .
. - Oblicz cosinus kąta
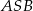 jeżeli
jeżeli 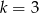 i
i 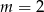 .
.
Dla każdej liczby 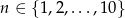 tworzymy funkcję
tworzymy funkcję 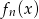 , której wykres powstaje przez przesunięcie wykresu funkcji
, której wykres powstaje przez przesunięcie wykresu funkcji 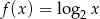 o wektor
o wektor ![[0 ,−n ]](https://img.zadania.info/zes/0075447/HzesT33x.gif) .
.
- Oblicz sumę wszystkich miejsc zerowych funkcji
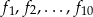 .
. - Wyznacz miejsce zerowe funkcji
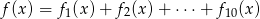 .
.
Wyznacz iloraz niezerowego ciągu geometrycznego, w którym suma 10 początkowych wyrazów jest 5 razy większa od sumy pierwszych 5 wyrazów.
Wykres funkcji 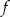 , określonej dla
, określonej dla 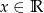 następującym wzorem
następującym wzorem
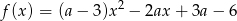
przecina dodatnią półoś 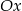 w dwóch różnych punktach.
w dwóch różnych punktach.
- Oblicz wartość wyrażenia
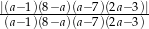 .
. - Uzasadnij, że dla każdych dwóch liczb rzeczywistych
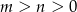 spełniona jest nierówność
spełniona jest nierówność 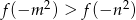 .
.
Na loterii jest  losów, w tym 4 wygrywające. Kupujemy 2 losy. Dla jakiej liczby
losów, w tym 4 wygrywające. Kupujemy 2 losy. Dla jakiej liczby  prawdopodobieństwo otrzymania co najmniej jednego losu wygrywającego jest równe
prawdopodobieństwo otrzymania co najmniej jednego losu wygrywającego jest równe 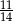 ?
?

