Zadanie nr 1524461
Punkty 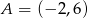 i
i 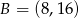 należą do wykresu funkcji
należą do wykresu funkcji 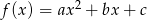 . Funkcja
. Funkcja 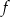 ma dwa miejsca zerowe, a wierzchołek paraboli będącej jej wykresem należy do prostej
ma dwa miejsca zerowe, a wierzchołek paraboli będącej jej wykresem należy do prostej 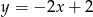 . Znajdź wzór tej funkcji.
. Znajdź wzór tej funkcji.
Rozwiązanie
Sposób I
Informacja o punktach na paraboli daje nam równania
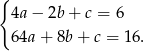
Odejmijmy od drugiego równania pierwsze (żeby skrócić  )
)
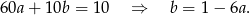
Z pierwszego równania mamy więc
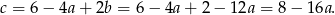
Teraz napiszmy warunek dotyczący wierzchołka paraboli.
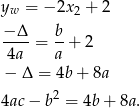
Podstawiamy teraz w tym równaniu wcześniej wyliczone wartości 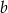 i
i  .
.
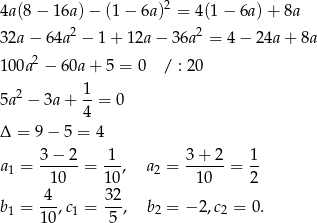
Łatwo sprawdzić, że pierwsze rozwiązanie daje parabolę, która nie ma miejsc zerowych (liczymy 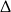 ę).
ę).
Sposób II
Skoro wierzchołek paraboli ma współrzędne 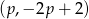 to funkcja ta ma postać (postać kanoniczna)
to funkcja ta ma postać (postać kanoniczna)
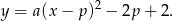
Parametry  i
i 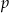 wyliczamy wstawiając podane punkty.
wyliczamy wstawiając podane punkty.
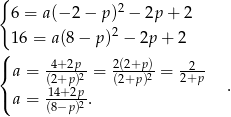
Po drodze założyliśmy, że 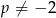 i
i 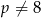 , ale łatwo sprawdzić, że te wartości
, ale łatwo sprawdzić, że te wartości 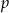 nie mogą być rozwiązaniem. Porównując otrzymane wartości
nie mogą być rozwiązaniem. Porównując otrzymane wartości  dostajemy równanie
dostajemy równanie
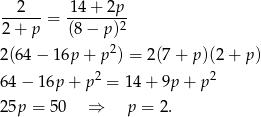
Zatem 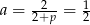 i funkcja ma postać
i funkcja ma postać
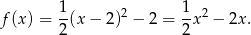
Odpowiedź: