Zadanie nr 4399566
Wykresy funkcji kwadratowych 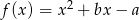 oraz
oraz 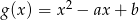 , gdzie
, gdzie 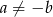 , przecinają się w punkcie leżącym na osi
, przecinają się w punkcie leżącym na osi 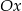 . Wiedząc, że osią symetrii wykresu funkcji
. Wiedząc, że osią symetrii wykresu funkcji 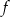 jest prosta o równaniu
jest prosta o równaniu 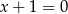 , oblicz
, oblicz 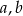 .
.
Rozwiązanie
Zacznijmy od drugiej informacji. Jeżeli osią symetrii wykresu funkcji 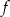 jest prosta
jest prosta 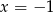 , to wierzchołek paraboli będącej wykresem funkcji
, to wierzchołek paraboli będącej wykresem funkcji 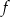 musi mieć pierwszą współrzędną równą -1. Zatem
musi mieć pierwszą współrzędną równą -1. Zatem
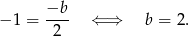
Mamy zatem 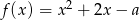 i
i 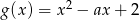 . Znajdźmy teraz punkty wspólne wykresów tych funkcji.
. Znajdźmy teraz punkty wspólne wykresów tych funkcji.
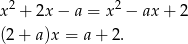
Z założenia wiemy, że 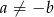 , więc
, więc 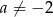 i dzieląc powyższe równanie przez
i dzieląc powyższe równanie przez 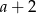 mamy
mamy 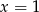 . Teraz pozostało sprawdzić, kiedy
. Teraz pozostało sprawdzić, kiedy 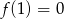 (bo punkt wspólny wykresów ma być na osi
(bo punkt wspólny wykresów ma być na osi 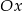 ).
).
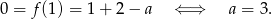
Na koniec obrazek dla ciekawskich.
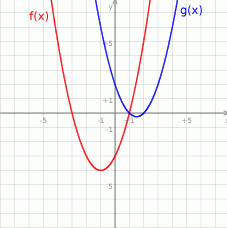
Odpowiedź: