/Szkoła średnia/Funkcje - wykresy/Parabola/Wzór z wykresu

Zadanie nr 4846210

Dodaj do ulubionych
Dodaj do rozwiązanych

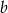Wyznacz wszystkie wartości parametrów a i b , dla których wykresy funkcji

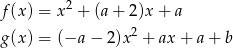
2 f(x ) = x + (a+ 2)x+ a g(x ) = (−a − 2)x2 + ax+ a+ b

przecinają się w dwóch różnych punktach leżących na osi 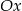Ox .

Rozwiązanie

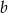Pytanie brzmi: kiedy dane równania mają te same pierwiastki? Spróbujemy najpierw wyznaczyć możliwe wartości a i b , a na koniec sprawdzimy, czy dla otrzymanych wartości każde z równań ma rzeczywiście dwa pierwiastki.

Jeżeli 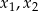x1,x2 są wspólnymi pierwiastkami danych równań, to na mocy wzorów Viète’a mamy

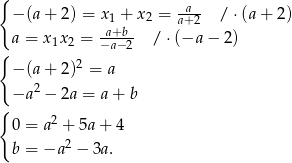
{ -a-- − (a+ 2 ) = x1 + x2 = a+ 2 / ⋅(a + 2) a = x1x2 = a+b-- / ⋅(−a − 2) { −a−2 − (a+ 2 )2 = a 2 { −a − 2a = a+ b 0 = a2 + 5a + 4 2 b = −a − 3a.

Rozwiązujemy otrzymane równanie kwadratowe

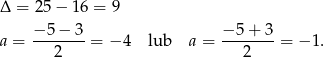
Δ = 25− 16 = 9 − 5 − 3 − 5 + 3 a = ------- = − 4 lub a = ------- = −1 . 2 2

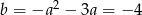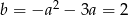Mamy wtedy odpowiednio 2 b = −a − 3a = − 4 i 2 b = −a − 3a = 2 .

W pierwszym przypadku otrzymujemy funkcje

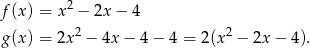
2 f(x) = x − 2x− 4 g(x) = 2x 2 − 4x− 4− 4 = 2(x2 − 2x − 4 ).

Ponadto 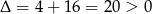Δ = 4+ 16 = 20 > 0 , więc każda z funkcji ma dwa miejsca zerowe.

W drugim przypadku mamy funkcje

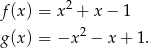
2 f(x) = x + x − 1 g(x) = −x 2 − x + 1 .

Tym razem 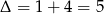Δ = 1+ 4 = 5 i tak jak poprzednio każda z funkcji ma dwa miejsca zerowe.  
Odpowiedź: 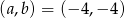(a,b) = (−4 ,−4 ) lub (a,b) = (−1 ,2)

Wersja PDF