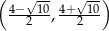Zadanie nr 7137106
Pewna parabola o wierzchołku 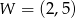 przecina oś
przecina oś 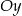 w punkcie
w punkcie 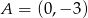 .
.
- Wyznacz postać ogólną funkcji kwadratowej
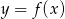 , której wykresem jest ta parabola.
, której wykresem jest ta parabola. - Rozwiąż nierówność
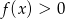 .
.
Rozwiązanie
- Korzystamy z postaci kanonicznej funkcji kwadratowej.
Skoro wiemy, w którym punkcie jest wierzchołek paraboli to ma ona postać.
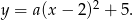
Teraz wystarczy podstawić w tej równości współrzędne punktu
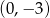
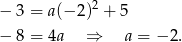
Pozostało wyznaczyć postać ogólną funkcji
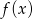 .
. 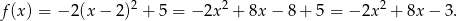
Odpowiedź: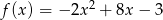
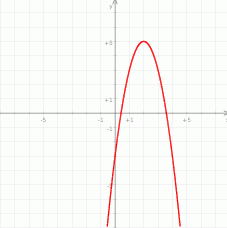
- Liczymy
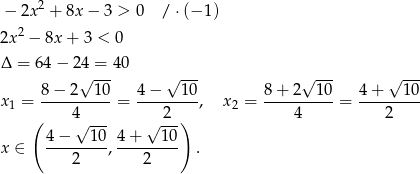
Odpowiedź: