Zadanie nr 7314190
Wykresem funkcji 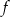 jest parabola, której wierzchołkiem jest punkt
jest parabola, której wierzchołkiem jest punkt 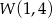 . Najmniejsza wartość funkcji
. Najmniejsza wartość funkcji 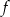 w przedziale
w przedziale 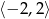 wynosi -5.
wynosi -5.
- Przedstaw wzór funkcji
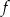 w postaci iloczynowej.
w postaci iloczynowej. - Rozwiąż nierówność
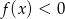 .
.
Rozwiązanie
-
Sposób I
Korzystając z postaci kanonicznej wiemy wiemy, że szukana funkcja musi mieć postać
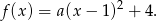
Dodatkowa informacja jaką mamy, to najmniejsza wartość funkcji w przedziale
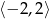 . Ponieważ ta wartość najmniejsza nie jest osiągana w wierzchołku paraboli, parabola ta musi mieć ramiona skierowane w dół.
. Ponieważ ta wartość najmniejsza nie jest osiągana w wierzchołku paraboli, parabola ta musi mieć ramiona skierowane w dół. 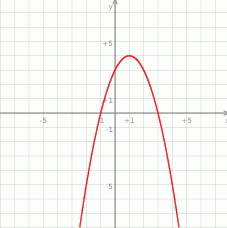
Ponadto, ponieważ jej wierzchołek jest w punkcie
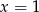 , a więc bliżej prawego końca przedziału
, a więc bliżej prawego końca przedziału 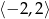 , wartość najmniejsza musi być osiągana w lewym końcu przedziału, czyli dla
, wartość najmniejsza musi być osiągana w lewym końcu przedziału, czyli dla 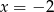 (rysunek). Zatem
(rysunek). Zatem 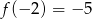 , co daje
, co daje 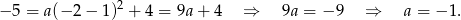
Zatem
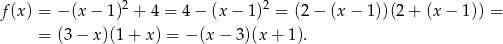
Sposób II
Niech
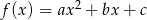 . Dane współrzędnych wierzchołka dają nam równania
. Dane współrzędnych wierzchołka dają nam równania 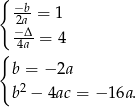
Tak jak w poprzednim sposobie stwierdzamy, że
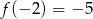 , co daje równanie
, co daje równanie 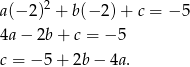
Wyliczoną wartość podstawiamy do drugiego z wcześniej wyliczonych równań i mamy układ
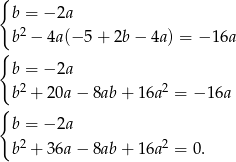
Podstawiamy
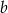 z pierwszego równania i mamy
z pierwszego równania i mamy 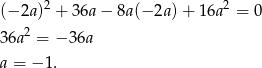
Stąd
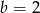 i
i 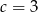 , czyli
, czyli 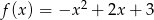 . Aby przedstawić ten trójmian w postaci iloczynowej musimy wyliczyć pierwiastki.
. Aby przedstawić ten trójmian w postaci iloczynowej musimy wyliczyć pierwiastki. 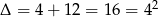 , co daje
, co daje 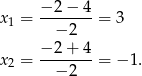
Zatem
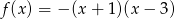
Odpowiedź: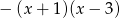
- Odczytujemy z wykresu,
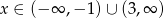 .
.
Odpowiedź: