Zadanie nr 7341790
Oblicz 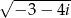 .
.
Rozwiązanie
Na początku możemy sprawdzić, czy przypadkiem liczba 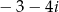 nie ma ładnej postaci trygonometrycznej – okaże się, że nie ma.
nie ma ładnej postaci trygonometrycznej – okaże się, że nie ma.
Sposób I
W takim razie liczymy wprost (dla pierwiastków stopnia 2 zawsze tak można). Szukamy takiej liczby 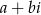 , że
, że
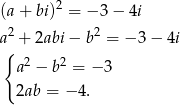
Z drugiego równania wyliczamy 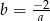 i wstawiamy do pierwszego równania (tu jest ważne, że
i wstawiamy do pierwszego równania (tu jest ważne, że 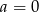 nie daje rozwiązania).
nie daje rozwiązania).
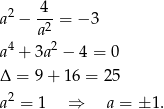
Pamiętając o tym, że 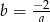 otrzymujemy dwa pierwiastki
otrzymujemy dwa pierwiastki
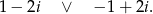
Sposób II
Tym razem jednak spróbujmy wykorzystać postać trygonometryczną. Mamy
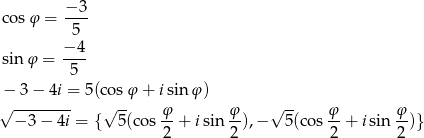
Aby policzyć żądany pierwiastek, musimy więc wyliczyć 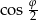 i
i 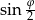 . Da się to łatwo zrobić korzystając ze wzorów.
. Da się to łatwo zrobić korzystając ze wzorów.
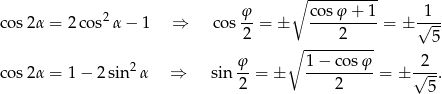
Aby ustalić znaki tych wyrażeń zauważmy, że 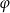 jest w III ćwiartce, zatem
jest w III ćwiartce, zatem 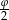 jest w II ćwiartce. Zatem
jest w II ćwiartce. Zatem
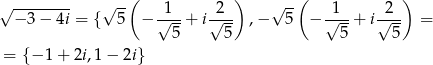
Odpowiedź: