/Konkursy/Zadania/Geometria/Planimetria/Romb/Różne

Zadanie nr 3027522

Dodaj do ulubionych
Dodaj do rozwiązanych

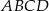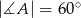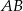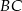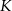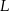Kąt ostry rombu ABCD ma miarę ∘ |∡A | = 6 0 . Na bokach AB i BC wybrano punkty K i L w ten sposób, że 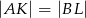|AK | = |BL | . Uzasadnij, że trójkąt 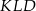KLD jest trójkątem równobocznym.

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

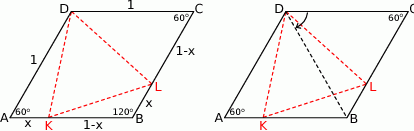
Sposób I

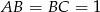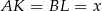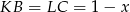Przyjmijmy, że AB = BC = 1 i oznaczmy AK = BL = x . Wtedy KB = LC = 1 − x .

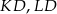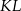Wyliczymy długości odcinków KD ,LD i KL z twierdzenia cosinusów.

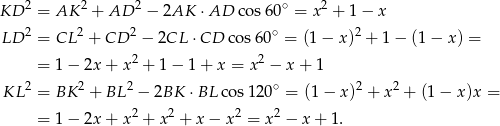
2 2 2 ∘ 2 KD = AK + AD − 2AK ⋅AD co s60 = x + 1 − x LD 2 = CL 2 + CD 2 − 2CL ⋅CD cos 60∘ = (1 − x)2 + 1 − (1 − x) = = 1 − 2x + x2 + 1− 1 + x = x2 − x + 1 2 2 2 ∘ 2 2 KL = BK + BL − 2BK ⋅BL cos 120 = (1 − x) + x + (1 − x)x = = 1 − 2x + x2 + x2 + x− x2 = x2 − x + 1.

Zatem rzeczywiście wszystkie boki trójkąta 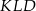KLD mają tę samą długość.

Sposób II

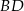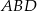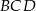Dorysujmy przekątną BD . Trójkąty ABD i BCD są równoramienne i mają kąt 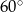∘ 60 , czyli są równoboczne.

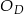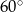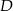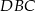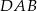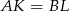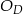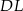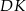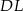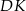Rozważmy obrót OD o kąt 60∘ wokół punktu D . Obrót ten przeprowadza trójkąt DBC na DAB . Ponadto, ponieważ AK = BL , obrót OD przekształci odcinek DL na DK . W takim razie odcinki DL i DK mają tę samą długość (bo rożnią się o obrót), oraz przecinają się pod kątem 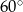∘ 6 0 (bo obrót o 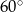∘ 60 przeprowadza jeden na drugi). To oznacza, że trójkąt 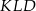KLD jest równoramienny z kątem 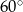60∘ między ramionami. Jest to więc trójkąt równoboczny.

Wersja PDF